Visual Factor in VINS-Fusion

projectionOneFrameTwoCamFactor §

Parameters to be optimised:

1. $[P_{b_i}^w,q_{b_i}^w]$ : SE(3) pose of body in frame i
2. $[P_{b_j}^w,q_{b_j}^w]$ : SE(3) pose of body in frame j
3. $[p_c^b,q_c^b]$: Extrinsic parameter between body and camera
4. ${\lambda }_l$: inverse depth, it is the depth of feature in frame i
5. $t_d$: time difference between camera & imu

$$\begin{array}{rl}residuals& =measurement-result\_from\_projection\\ r_c& =\left[\begin{array}{c}{u}_j-\frac{X_j}{Z_j}\\ v_j-\frac{Y_j}{Z_j}\end{array}\right]\end{array}$$

residual = (pts_camera_j / dep_j).head<2>() - pts_j_td.head<2>();
residual = sqrt_info * residual;

There are 4 Jacobian in Evaluate function.

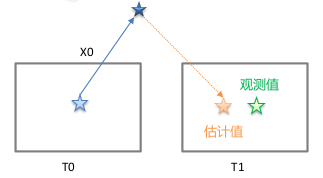
• For feature point that is first observed in camera at frame i and project it into camera at frame j

  $$\left[\begin{array}{c}{X}_{c_j}\\ Y_{c_j}\\ Z_{c_j}\\ 1\end{array}\right]=T_b^c\ast T_w^{b_j}\ast T_{b_i}^w\ast T_c^b\ast \left[\begin{array}{c}{X}_{c_i}\\ Y_{c_i}\\ Z_{c_i}\\ 1\end{array}\right]\text{\hspace{1em}(1)}$$

  Since $\frac{1}{\lambda }=Z_{c_i}$ and using the projection function, let’s further modify Equation(1)

  $$\left[\begin{array}{c}{X}_{c_j}\\ Y_{c_j}\\ Z_{c_j}\\ 1\end{array}\right]=T_b^c\ast T_w^{b_j}\ast T_{b_i}^w\ast T_c^b\ast \left[\begin{array}{c}\frac{1}{\lambda }{u}_{c_i}\\ \frac{1}{\lambda }{v}_{c_i}\\ \frac{1}{\lambda }\\ 1\end{array}\right]\text{\hspace{1em}(2)}$$

  Expand the Equation(2) by $T_b^a{P}^b=R_b^a{P}^b+t_b^a$,

  $$f_{c_j}=\left[\begin{array}{c}{X}_{c_j}\\ Y_{c_j}\\ Z_{c_j}\end{array}\right]\begin{array}{rl}& =R_b^c{R}_w^{b_j}{R}_{b_i}^w{R}_c^b\frac{1}{\lambda }\left[\begin{array}{c}{u}_{c_i}\\ v_{c_i}\\ 1\end{array}\right]\\ & +R_b^c(R_{b_j}^w(R_{b_i}^w{p}_c^b+p_{b_i}^w-p_{b_j}^w)-p_c^b)\end{array}\text{\hspace{1em}(3)}$$

  What is our target? To find out the derivative of residual, which is the Jacobian of Lie Group

  

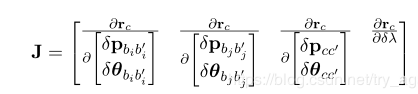
  By using Chain Rule: $$ \frac{\delta r_c}{\delta P} = \frac{\delta r_c}{\delta f_{c_j}}*\frac{\delta f_{c_j}}{\delta P} \tag{4}

  P consists of all the parameters that we want to optimise: [note: $t_d$ is missing in the picture]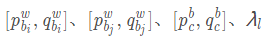 

​ For the first term in Equation(4), in code it is declare as reduce

$$\frac{\delta r_c}{\delta f_{c_j}}=\left[\begin{array}{ccc}\frac{1}{Z_{c_j}}& 0& -\frac{X_{c_j}}{Z_{c_j}^2}\\ 0& \frac{1}{Z_{c_j}}& -\frac{Y_{c_j}}{Z_{c_j}^2}\end{array}\right]\text{\hspace{1em}(5)}$$

​ For the second term in Equation(4), let’s take the derivative for each parameters

1. Jacobian[0] $$ \frac{\delta f_{c_j}} {\delta \begin{bmatrix} \delta p_{b_i}^w \ \delta \theta_{b_i^w} \end{bmatrix} } §

   \begin{bmatrix} \frac{\delta f_{c_j}}{\delta p_{b_i}^w} , \frac{\delta f_{c_j}}{\delta \theta_{b_i}^w} , \end{bmatrix}

   $$Le{t}^{\prime }stakederivativeexampleforthefirstterm,$$

   \frac{\delta f_{c_j}}{\delta p_{b_i}^w} = R_b^cR_w^{b_j}

2. Jacobian[1]

   Eigen::Matrix<double, 3, 6> jaco_j;
   jaco_j.leftCols<3>() = ric.transpose() * -Rj.transpose();
   jaco_j.rightCols<3>() = ric.transpose() * Utility::skewSymmetric(pts_imu_j);

   $$jaco\_j_{3x6}=\left[\begin{array}{cccccc}|& -& |& |& -& |\\ |& \frac{\delta f_{c_j}}{\delta p_{b_i}^w}& |& |& \frac{\delta f_{c_j}}{\delta q_{b_i}^w}& |\\ |& -& |& |& -& |\end{array}\right]$$

3. Jacobian[2]: extrinsic parameter between body and camera

4. Jacobian[3]: about feature

   $$\begin{array}{rl}\frac{\partial {\mathbf{r}}_{\mathcal{C}}}{\partial {\lambda }_l}& =\frac{\partial {\mathbf{r}}_{\mathcal{C}}}{\partial p_l^{c_j}}\frac{\partial p_l^{c_j}}{\partial {\lambda }_l}\\ \text{where }\frac{\partial p_l^{c_j}}{\partial {\lambda }_l}& =R_b^c{R}_w^{b_j}{R}_{b_i}^w{R}_c^b{\pi }_c^{-1}\left(\left[\begin{array}{c}{u}_l^{c_i}\\ v_l^{c_i}\end{array}\right]\right)\frac{1}{{\lambda }_l^2}\end{array}$$

5. Jacobian[4]: about time $t_d$

Reference §

1. VINS-MONO理论学习---紧耦合后端非线性优化
2. VINS 系统中的视觉重投影因子
3. VINS_FUSION入门系列－优化optimization