Column Space

Given a matrix $A$, all the linear combinations of the columns of $A$ form a Subspaces. This is the column space $C(A)$.

For example, if $A=\left[\begin{array}{cc}0& 1\\ -1& 0\\ 1& 0\end{array}\right]$, the column space of $A$ is the plane through the origin in ${\mathbb{R}}^3$ containing $\left[\begin{array}{c}0\\ -1\\ 1\end{array}\right]$ and $\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]$.

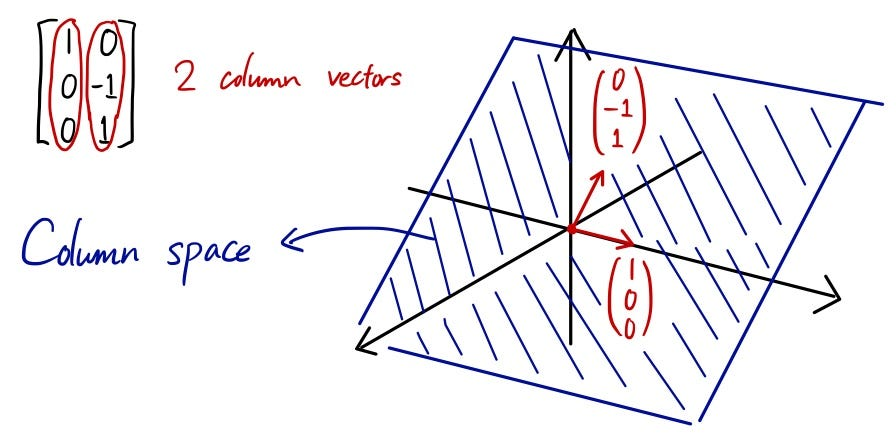
Column space of $A$ and solving $A\mathbf{x}=\mathbf{b}$ §

Given a matrix $A$, the system of linear equations $A\mathbf{x}=\mathbf{b}$ is solvable exactly when $\mathbf{b}$ is a vector in the column space of $A$.

Nullspace of $A$ §

The Nullspace* of a matrix $A$ is the collection $x$ to the equation $A\mathbf{x}=0$

For example,

$$\left[\begin{array}{ccc}1& 1& 2\\ 2& 1& 3\\ 3& 1& 4\\ 4& 1& 5\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\right],$$

the Nullspace $N(A)$ consists of all multiples of $\left[\begin{array}{c}1\\ 1\\ -1\end{array}\right]$. This Nullspace is a line in ${\mathbb{R}}^3$.

Attention, a nullspace is a vector space because it obviously satisfies the requirements about addition and scale multiplication. That is to say that any sum or multiple of solutions of $A\mathbf{x}=0$ is also a solution: $A({\mathbf{x}}_1+{\mathbf{x}}_2)=0+0=0$ and $A(c\mathbf{x})=cA\mathbf{x}=c0=0$.

Other values of $\mathbf{b}$ §

The solutions to the equation:

$$\left[\begin{array}{ccc}1& 1& 2\\ 2& 1& 3\\ 3& 1& 4\\ 4& 1& 5\end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\end{array}\right]=\left[\begin{array}{c}1\\ 2\\ 3\\ 4\end{array}\right],$$

do not form a subspace. This conclusion is obvious since the zero vector is not a solution to the equation. Actually, the set of solutions forms a line in ${\mathbb{R}}^3$ that pass through the points $\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]$ and $\left[\begin{array}{c}0\\ -1\\ 1\end{array}\right]$, but not $\left[\begin{array}{c}0\\ 0\\ 0\end{array}\right]$.