Subspaces

We say that a subset $U$ of a vector space $V$ is a subspace of $V$ if $U$ is a vector space under the inherited addition and scalar multiplication operations of $V$.

• the origin,
• a line through the origin,
• a plane through the origin,
• all of ${\mathbb{R}}^3$.

Consider a plane P in ${\Re }^3$ through the origin:

$$\begin{array}{rl}ax+by+cz& =0\\ \left(\begin{array}{ccc}a& b& c\end{array}\right)\ast \left(\begin{array}{c}x\\ y\\ z\end{array}\right)& =0\\ MX& =0\end{array}$$

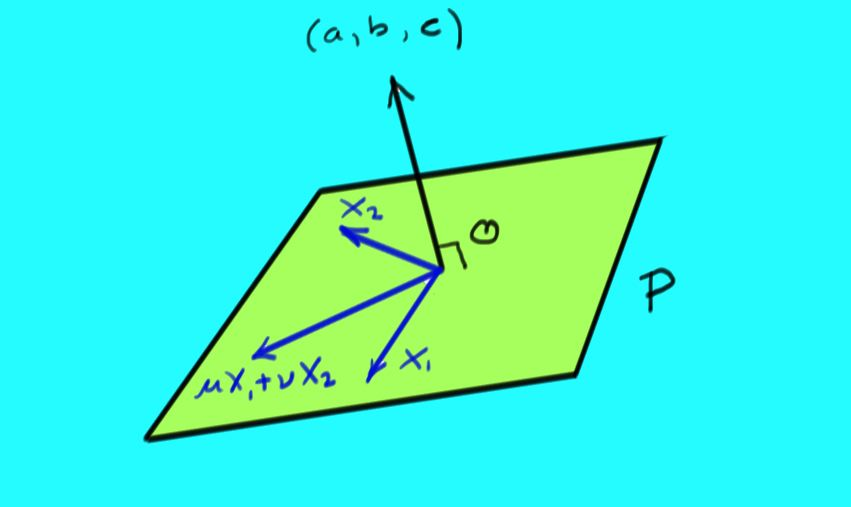
If $X_1$ and $X_2$ are both solutions to $MX=0$, then by linearity of Matrix Multiplication, so is $\mu X_1+\upsilon X_2$:

$$M(\mu X_1+\upsilon X_2)=\mu M{X}_1+\upsilon M{X}_2=0$$